魔数不魔 · 令人着迷的快速平方根倒数算法

发表于 2021-08-22 更新于 2022-10-08 分类于技术文档阅读次数：本文字数： 3.7k 阅读时长 ≈ 3 分钟

想必大家一定或多或少听过一个历史悠久的快速计算平方根倒数的算法，这个算法由于出现在《雷神之锤III竞技场》源代码中而被人们所熟知，每次看到这个算法，内心除了惊呼NB外，对其背后的原理一脸懵逼，加上最近正好在学习IEEE754标准，于是就索性利用周末寻找资料，看看远古时期的那些大神们是如何利用自己的智慧挑战硬件的极限，也看看后面的大神们是如何探究和揭秘这个算法的。

神一样的算法

/*
** float q_rsqrt( float number )
** 注：计算根号x的倒数
*/
float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;                       // evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed
	return y;
}

前序知识

由于这个算法涉及浮点数标准以及设备的字节序，因此需要有一些事前知识需要准备，这里只简单介绍一下 IEEE754 对单精度浮点数的表示方式（只涉及浮点正规数），至于字节序由于比较简单，这里不赘述，我们只考虑常见的小端。

浮点格式是一种数据结构，用于指定包含浮点数的字段、这些字段的布局及其算术解释。IEEE 754 明确规定了单精度浮点格式和双精度浮点格式，并为这两种基本格式分别定义了一组扩展格式，这里只简单介绍一下单精度浮点数：

IEEE 单精度格式具有 24 位有效数字精度，并总共占用 32 位，由三个字段组成：

23 位小数 f
8 位偏置指数 e
1 位符号 s

这些字段连续存储在一个 32 位字中，如下图所示：

0:22 位包含 23 位小数 f，其中第 0 位是小数的最低有效位，第 22 位是最高有效位；23:30 位包含 8 位偏置指数 e，第 23 位是偏置指数的最低有效位，第 30 位是最高有效位；最高的第 31 位包含符号位 s

这里包含几个概念：

所有的浮点数都是二进制浮点数，举个例子：10.625 中，10 用二进制表示为1010，代表 $1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0$，而小数位 0.625，类似于十进制的表示方式，可以认为其值为 $1 \times 2^{-1} + 0 \times 2^{-2} + 1 \times 2^{-3}$，即 0.101，最终，10.625的二进制表示就是 1010.101。回到上面的介绍中，可以看到浮点数是由浮点位和指数位构成的，因此用科学计数法表示，可以写成 $1.010101 \times 2^3$，对于本文涉及的浮点值肯定是正数，因此符号位恒为 0
指数偏差：上面得到的指数 e 并不是直接以二进制形式存储在23:30 位中，实际上在浮点数中，指数存储的值通过指数偏差从实际值进行偏移，进行偏置是因为指数必须是有符号值才能表示微小值和巨大值，但是通常用补码表示有符号值，这会增加比较的难度，为了解决这个问题，指数被存储为适合比较的无符号值，并且在解释时通过减去偏差将其转换为有符号范围内的指数，对于 float来说，这里的偏差就是 127
前导有效数位：前面介绍，单精度浮点值精度是 24 位，但为什么只有 23 位用于存储小数部分呢？这里有一个隐含规定，对于绝大部分单精度浮点数，有效数字可以表示为 1.01010101 这种形式，我们称之为正规数，针对这类数字，我们已经假定了是以 1 开头的，这个假定在 IEEE 单精度浮点值中是可以根据 e 的值推断出来的，被隐含在 e 中（即：0 < e < 255 的情况下假定是1），23 位数字加上隐含的1位有效数位，共 24 位精度
格式位模式：对于单精度正规数，其浮点值为：$-1^s \times 2^{e-127} \times 1.f$

算法解析

我们的目标是计算 $f(x) =\frac{1}{ \sqrt{x}}$，我们假设小数位是m, 指数位是e，实际存储的指数内容的十进制表示是 E（即：23:30 位对应的整数），实际存储的小数内容是 M（即：0:22 位对应的整数），通过前序知识，我们可以知道 :

方程 1：
$$
x = (1+m) \times 2^e
$$

方程 2：
$$
E = e + 127
$$
参见前面的指数偏差介绍

方程 3：
$$
M = 2^{23} \times m
$$
即小数位如果解释为整数，二者的值会相差 23 位

我们对目标函数取 2 的对数，可以得到下面的结果：

方程 4：
$$
\log_2y = - \frac{1}{2} \log_2x
$$

上面公式中，x 是已知的参数，x 和 y 都是对应的浮点值，我们将 x 和 y 全部按照 方程1 表示成浮点值表示：

方程 5：
$$
x = (1+m_x) \times 2^{e_x}
$$
$$
y = (1+m_y) \times 2^{e_y}
$$

带入目标函数对数表示的 方程4 中，可以得到：

方程 6：
$$
\log_2{(1+m_y)} + e_y = - \frac{1}{2} [\log_2{(1+m_x)} + e_x]
$$

这一步的目的是把乘法运算表示为加法运算。

天才假设

观察函数 $f(x) = log_2{(1+x)}$（红色图像），在 (0, 1) 作用域下，其函数图像很像 $f(x) = x + \sigma $（蓝色图像）这是这个算法中第一个让人脑洞大开的天才假设

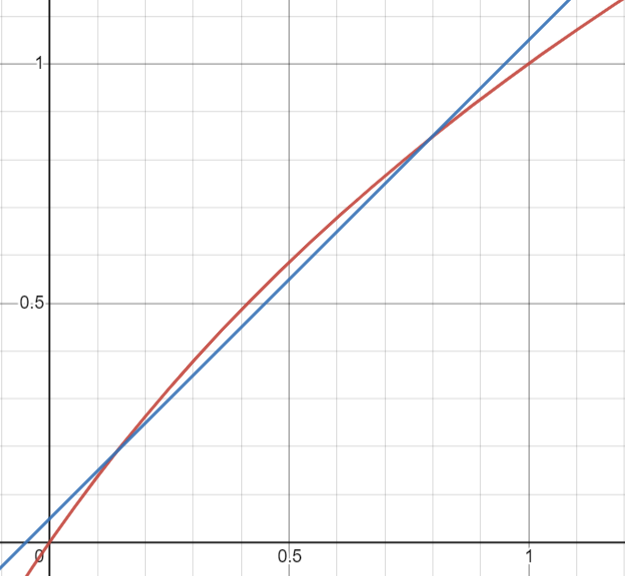
因此，我们得到了近似方程：

方程 7：
$$
\log _2{(1+x)} \cong x+\sigma
$$
其中的 $\sigma$是一个特定的常数

将其带入 方程6 可以得到一个近似方程 注：(0, 1) 作用域下：

方程 8：
$$
\sigma + m_y + e_y \cong - \frac{1}{2} (\sigma + m_x + e_x)
$$

上述公式中，m 和 e 都是实际的指数和小数，那么其和实际在二进制中存储的数据的整数表示有什么关系呢？参考 方程2 和 方程3，带入上面的 方程8，即可得到下面的方程：

方程 9：
$$
\frac{M_y}{2^{23}} + \sigma + E_y - 127 \cong - \frac{1}{2} (\frac{M_x}{2^{23}} + \sigma + E_x - 127)
$$
整理得：
$$
M_y + 2^{23} \times E_y \cong \frac{3}{2} \times 2^{23} \times (127-\sigma) - \frac{1}{2} (M_x + 2^{23} \times E_x)
$$

可以看到，左右两边都产生了 $M + 2^{23} \times E$ 这样的式子，这里的 M 和 E 分别对应二进制存储中的 0:22 和 23:30位整数内容，如果我们把 M 和 E 不理解成孤立的两个数字，而是统一当成一个 32 位的整数（注：第一位符号位始终为 0），会有什么样的结果呢？

神来之笔

举个例子：$123456 = 123 \times 10^3 + 456$ ，这恰好就类似于 $ 2^{23} \times E + M$，这里是本算法第二个神来之笔。也就是说，上述的 M 和 E 的组合，正好对应于浮点数据结构的整型解释，替换后得到下面的方程：

方程 10：
$$
y_{int} \cong \frac{3}{2} \times 2^{23} \times (127-\sigma) - \frac{1}{2} (x_{int})
$$

这个式子告诉我们，本来是一个浮点数，按照 IEEE 754 标准存储，把它按照整数解释之后，竟然满足上面的近似关系，这不就是代码中：i = 0x5f3759df - ( i >> 1 )的方程吗？

至于这个公式中的常量$\frac{3}{2} \times 2^{23} \times (127-\sigma)$取多少合适，可以通过穷举或者其他手段获取一个合适的值，这也是一个很有趣的课题，本算法中的 0x5f3759df就是一个比较合适的常量了，其中 $\sigma \cong 0.0450465$，这个值的最初起源可能会永远成为计算机世界的未解之谜。

至于后续的牛顿法，随便一本大学的数值分析课本都讲的很清楚了，这里就不赘述了。

牛顿法：
$$
{x_{n+1}=x_{n}-{\frac {f(x_{n})}{f’(x_{n})}}}
$$
化简整理后，对应代码 y * ( threehalfs - ( x2 * y * y ) )

后记

远古时期，计算机领域的天才们，通过计算和观察，发现将浮点数存储结构按照整形进行解释后，竟然存在某些规律，通过整数变换后，得到的值又可以在继续当成浮点数看待。虽然从最终的原理解释上看，算法本质并不复杂，但是如何从繁杂的表象中探究出深层的关系，才是我们需要学习和思考的地方。
写到这里，又想起了研究生时期去图书馆翻书查找各种文档，最终用C++实现Levenberg-Marquard 算法对某发动机的试验数据进行优化的日子了，一样的近似替换，一样的迭代优化，最终却停留于表象，没有找到最优的解法，还是比较遗憾的。

by wlop